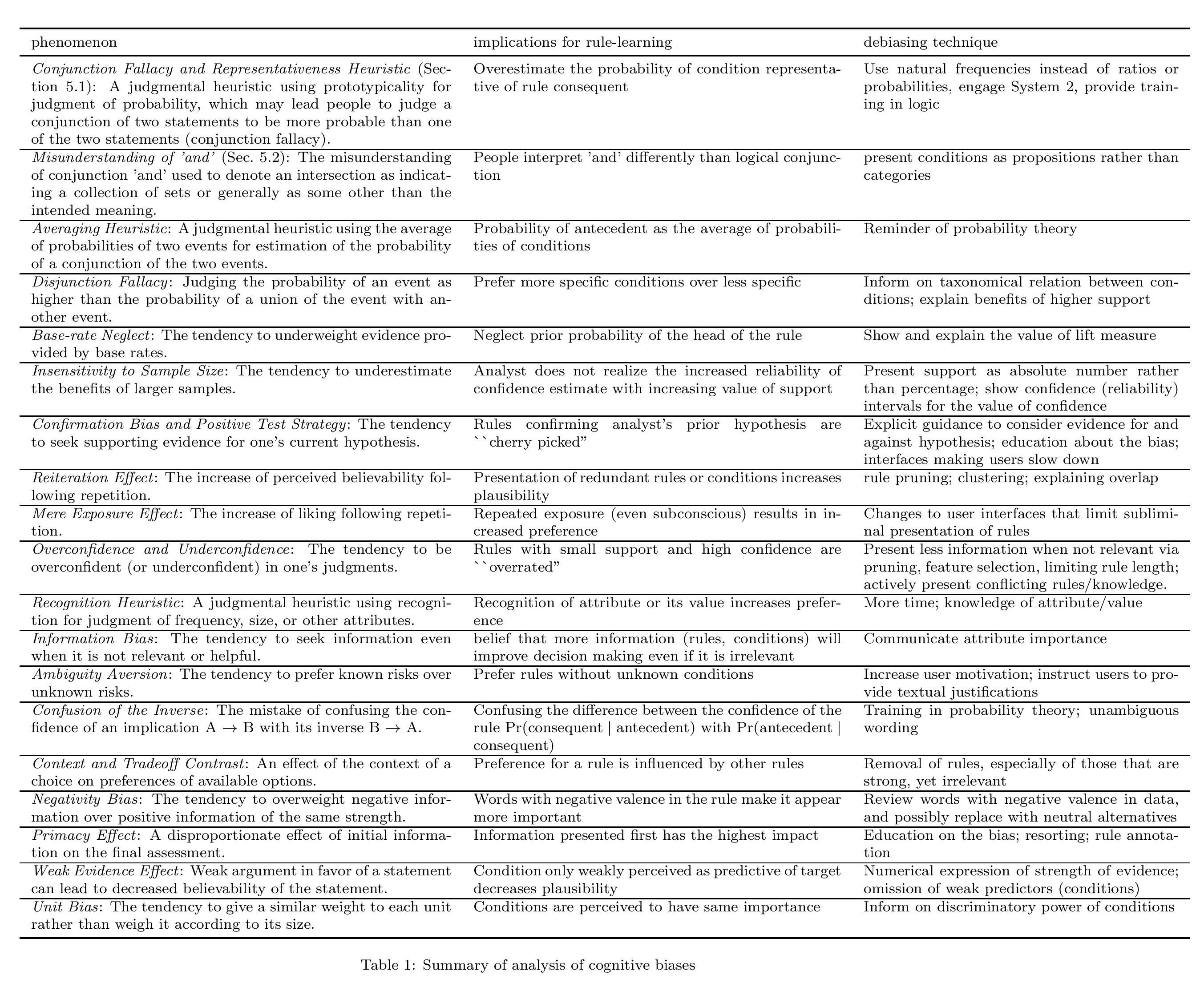
Double Elimination Brackets
Fighting game tournaments traditionally use double elimination brackets. In single elimination brackets, you would keep playing matches until you lose, after which you’re eliminated from the tournament. In a double elimination tournament, you’re instead put into a loser’s bracket (or lower bracket). If you win here, you’re paired off with the losers from the winner’s bracket (or upper bracket). It’s only if you lose a second time that you’re eliminated from the tournament. This gives competitors a second chance and makes for a more satisfying experience given fighting games can be quite volatile, and a loss might not represent a major difference in skill.
Finding Round Count
To esimate the amount of time required to run a double elimination (DE) bracket with $N$ entrants, we can calculate how many rounds we’d have to run. This ignores practical issues, since competitors cannot instantaneously teleport to the next available station once their match is over, and a match could take a variable amount of time to complete (say, $t_\text{match}$). However, if we have the number of rounds $R$, we can estimate the total time taken to run a tournament $T_\text{total}$ as
\[T_\text{total} = R \times t_\text{match}\]Let’s first assume we have $N=2^m$ entrants. How a DE bracket works can be summarized by the table below. The entry under each bracket shows how many entrants it has, describing the flow of competitors.
| Round | Upper Bracket | Lower Bracket |
|---|---|---|
| Round 1 | $2^m \to (2^{m-1}, 2^{m-1})$ | $-$ |
| Round 2 | $2^{m-1} \to (2^{m-2}, 2^{m-2})$ | $2^{m-1} \to (2^{m-2}, -)$ |
| Round 3 | $-$ | $2^{m-2} + 2^{m-2} \to (2^{m-2}, -)$ |
| Round 4 | $2^{m-2} \to (2^{m-3}, 2^{m-3})$ | $2^{m-2} \to (2^{m-3}, -)$ |
| Round 5 | $-$ | $2^{m-3} + 2^{m-3} \to (2^{m-3}, -)$ |
| $\vdots$ | $\vdots$ | $\vdots$ |
| Winner’s Final | $2 \to (1, 1)$ | $2 \to (1, 1)$ |
| Loser’s Final | $-$ | $1 + 1 \to (1, -)$ |
| Grand Final | $2 \to (1, -)$ | |
| Grand Final Reset | $-$ | $2 \to (1, -)$ |
The general pattern is easy to see. Skipping the first round, for every round in the upper bracket, there must be $2$ rounds in the lower bracket - one to get the number of entrants equal to the number of losers from the upper bracket, and two to match the new loser’s to the previous losers. Including the initial round, grand finals and possible reset, we have $2$ additional rounds plus a possible extra. Thus, we get -
\[R = \left\{\begin{array}{lr} 2 \times (\left\lceil\lg N\right\rceil - 1) + 2, \text{ no grand finals reset} \\ 2 \times (\left\lceil\lg N\right\rceil - 1) + 3, \text{ grand finals reset} \end{array}\right\}\]For $N = 16$ as in the figure above, this formula correctly predicts $R = 9$. For $N = 11$ as in this tournament, this formula still correctly predicts $R = 8$ since the higher seeded entrants are usually given byes into the next round, which evens out the round count.
DocMassacre is a senior electrical engineer at Raytheon Technologies who’s also an avid Tekken player (and holds a doctorate!). He posted a series of tweets exploring the probability of taking an entire tournament assuming a fixed probability of winning any particular set against anyone. In particular, he makes four claims -
- In an $N=64$, single elimination bracket, FT2 rounds, FT2 matches, $50\%$ chance of winning a round against anyone, the probability of taking the entire tournament is $1.8\%$.1
- To have a $50\%$ probability of winning an $N=64$, single elimination bracket with FT2 rounds, FT2 matches, it would take having a $71\%$ chance of winning any round against anyone you face.2
- In an $N=64$, single elimination bracket, FT2 rounds, FT2 matches, $40\%$ chance of winning a round against anyone, the probability of taking the entire tournament is $0.07\%$.3
- In an $N=64$, single elimination bracket, FT2 rounds, FT2 matches, $30\%$ chance of winning a round against anyone, the probability of taking the entire tournament is $\approx 10^{-6}$.1
Of course, I wanted to write a script myself to find these numbers and cross-check them. DocMassacre used a simple Monte Carlo simulation4 to find these numbers, but I believe we can do this analytically using some combinatorics.
Probability of winning an FT{N}
Given a series of matches between two competitors, say guessing correctly on a coin flip, what’s the probability of one competitor reaching $N$ wins first? The motivation behind solving this problem is that we can model the probability of winning a single game (Tekken games are usually FT3 rounds), and a single match (Tekken matches are usually FT2 or FT3) in this fashion.
The number of wins achieved is a random variable $X$ that follows the binomial distribution $X \sim B(n, p)$, where $n$ is the $N$ in our “FT{N}”, and $p$ is the probability of winning that game (or round, or match).
If we have $n$ wins, we want to distribute $l \in [0, n)$ losses among them (but none after the final win, since the game would be over). This is a fairly standard combinatorics problem. If we want to distribute $n$ identical objects into $r$ groups, such that each group can have $0$ or more ($\leq n$) objects, then the number of ways to do so is ${n+r-1 \choose r-1}$. Let’s say we have $l$ losses. We want to distribute those $l$ losses between our $n - 1$ wins (which forms $n - 1 + 1 = n$ groups). The number of ways to do so is thus ${l+n-1 \choose n-1}$.
Given the probability of winning a game as $p$, we can find the probability of winning a FT{N} as -
\[\Pr[\text{FT}\{N\}] = \sum_{l=0}^{n - 1} p^n (1-p)^{l} {l+n-1 \choose n-1}\]I wrote a Python script to implement this formula. I also coded up DocMassacre’s Monte Carlo simulation to provide a comparison, using 1000 trials.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import math
import random
from typing import Callable
random.seed(1)
FTN_FN = Callable[[int, float, int], float]
TRIALS = 10**3
ROUNDS_PER_GAME = 2 # number of rounds to win in a game, to win the game
FT2_GAMES = 2 # number of games to win in an FT2 set, to win the set
FT3_GAMES = 2 # number of games to win in an FT3 set, to win the set
def ftn_prob(n: int, win_prob: float) -> float:
prob: float = 0.0
for losses in range(0, n):
prob += (win_prob ** n) * ((1 - win_prob) ** losses) * math.factorial(n - 1 + losses) / (math.factorial(n - 1) * math.factorial(losses))
return prob
def sim_prob(n: int, win_prob: float, trials: int=TRIALS) -> float:
m: int = 0
for _ in range(0, trials):
r = 0
for _ in range(n + 1):
r += 1 if (random.random() < win_prob) else -1
m += 1 if (r > 0) else 0
return m / trials
def ft1_prob(ftn_fn: FTN_FN, round_win_prob: float) -> float:
return ftn_fn(ROUNDS_PER_GAME, round_win_prob)
def ft2_prob(ftn_fn: FTN_FN, round_win_prob: float) -> float:
return ftn_fn(FT2_GAMES, ft1_prob(ftn_fn, round_win_prob))
def ft3_prob(ftn_fn: FTN_FN, round_win_prob: float) -> float:
return ftn_fn(FT3_GAMES, ft1_prob(ftn_fn, round_win_prob)) # TODO: change back to 3
def n_man_bracket_prob(ftn_fn: FTN_FN, n: int, round_win_prob: float) -> float:
ft2s = math.floor(math.log2(n)) - 1
ft3s = 1
no_loss_prob = (ft2_prob(ftn_fn, round_win_prob) ** ft2s) * (ft3_prob(ftn_fn, round_win_prob) ** ft3s)
one_loss_prob = 0 # TODO:
total_prob = no_loss_prob + one_loss_prob
return total_prob
if __name__ == '__main__':
n: int = 64
for round_win_prob in (x * 0.01 for x in list(range(0, 70, 5)) + list(range(70, 101))):
print(f'{round_win_prob:.2f}\t{n_man_bracket_prob(ftn_prob, n, round_win_prob):.10f}\t{n_man_bracket_prob(sim_prob, n, round_win_prob):.10f}')
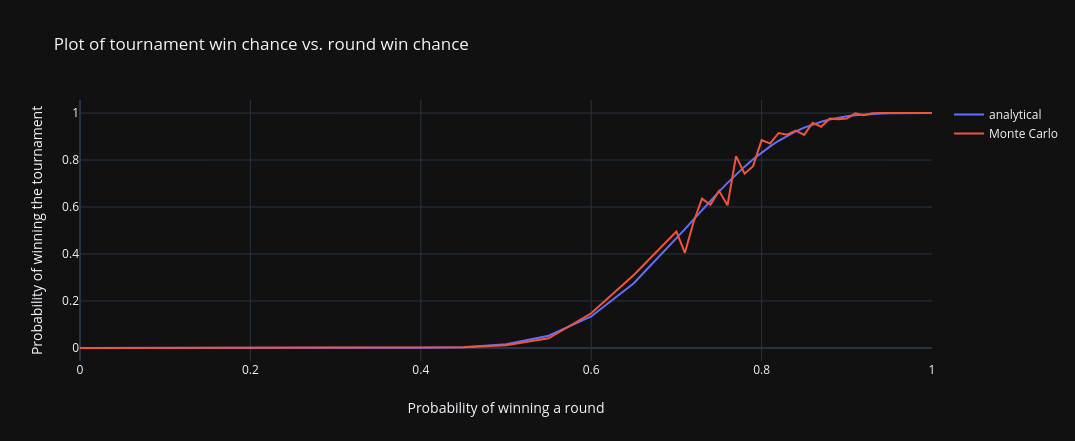
Here are the results -
Here are some comparisons to what DocMassacre found -
| Question | DocMassacre’s answer | Analytical answer | Monte Carlo answer |
|---|---|---|---|
| 1 | $0.018$ | $0.015$ | $0.011$ |
| 2 | $0.71$ | $0.71$ | $\sim 0.71$ |
| 3 | $0.0007$ | $0.0005$ | $0.0006$ |
| 5 | $0.000001$ | $0.000003$ | $0.000002$ |
The values are fairly similar, with the simulated values more or less agreeing with DocMassacre’s results (he might have used more trials). The simulations consistently overestimate the probability compared to the analytical values, though, especially for the lower win probability rates (till $\approx 0.7$).
We can modify the script to account for double elimination brackets as is used in actual Tekken tournaments. I will explore this later, however.
-
https://twitter.com/luria_justin/status/1627749352373424134 ↩ ↩2 ↩3
-
https://twitter.com/luria_justin/status/1627786360189775872 ↩ ↩2
-
https://twitter.com/luria_justin/status/1627786892648259585 ↩ ↩2
-
https://twitter.com/luria_justin/status/1628032344190853126 ↩
-
https://twitter.com/luria_justin/status/1627833348461678593 ↩